こんにちは。ニコラ・テスラを尊敬しているミーハーです。
今回は、プログラミング初心者の私が機械学習に挑戦して、実際に実践してみたので紹介します。
目次
目的
Pythonで機械学習を実践することによって、原理・プログラム内容を学び、さらなる発展的な機会学習に取り組みたいから
原理・理論
機械学習とは
人工知能の分野の1つで、人に備わる学習能力と同じような機能をコンピュータで再現しようとする技術のことです。
「人工知能」という言葉は、1965年にダートマス会議でジョン・マッカーシが命名したと言われています。
人工知能のブームは第1次、第2次、第3次の3段階に渡ってAIブームが起こりました。
2005年、アメリカの未来学者例・カーツワイルが、「自らを改良し続ける人工知能が生まれること。それが(端的にいうと)シンギュラリティだ」と発言しました。
そして、2006年にジェフリー・ヒントンらが提案したディープラーニングが、現在の激アツ第3次AIブームを巻き起こしたのです。
それから、月日がたった2015年。
囲碁プログラム「AlphaGo」が人間のプロ囲碁棋士に勝利したことにより、ディープラーニングは更に注目を集めています。
機械学習に利用するモジュール
scikit-learn
機械学習に必要な回帰、分類、クラスタリングなどのアルゴリズムを備えている。
NumPy
数値計算を高速に行うためのモジュール
NumPyの基本操作コード
# NumPyの基本操作
import numpy as np
a = np.array([0,1,2,3,4])
b = np.array([0,1,2,3,4,5]).reshape(2,3)
c = b*3
# 0を10個
d = np.zeros(10)
e = np.zeros(10).reshape(2,5)
# 軸の入れ替え(5,2)
# d.transpose(1,0)またはd.T
f = d.T
# 1を8個
g = np.ones(8)
# 乱数の配列
h = np.random.rand(10)
i = np.arange(10)
j = np.pi
print('a={}'.format(a))
print('a配列の2番目={}'.format(a[2]))
print('b={}'.format(b))
print('bの3倍={}'.format(c))
print('d={}'.format(d))
print('e={}'.format(e))
print('f={}'.format(f))
print('g={}'.format(g))
print('h={}'.format(h))
print('i={}'.format(i))
print('j={}'.format(j))
input()
(ouput)
a=[0 1 2 3 4]
a配列の2番目=2
b=[[0 1 2]
[3 4 5]]
bの3倍=[[ 0 3 6]
[ 9 12 15]]
d=[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
e=[[0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0.]]
f=[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
g=[1. 1. 1. 1. 1. 1. 1. 1.]
h=[0.88904965 0.92725078 0.31338365 0.53745743 0.74273041 0.69725689
0.2865491 0.89960714 0.85736175 0.36596312]
i=[0 1 2 3 4 5 6 7 8 9]
j=3.141592653589793
input()をつけているのは、pythonを実行したときにすぐにコマンドプロンプトが消えないようにするためです。
ベクトルや行列の計算コード
# ベクトルや行列の計算
import numpy as np
a = np.array([1,2,3,4])
b = np.array([3,4,5,6])
c = a*b
d = np.dot(a,b)
e = np.array([[2,3],[5,2]])
f = np.array([[5,6],[3,4]])
g = np.dot(e,f)
print('a={}'.format(a))
print('b={}'.format(b))
print('aとbのかけ算c={}'.format(c))
print('aとbのベクトルの内積 d={}'.format(d))
print('e={}'.format(e))
print('f={}'.format(f))
print('eとfの行列の積 g={}'.format(g))
input()
(output)
a=[1 2 3 4]
b=[3 4 5 6]
aとbのかけ算c=[ 3 8 15 24]
aとbのベクトルの内積 d=50
e=[[2 3]
[5 2]]
f=[[5 6]
[3 4]]
eとfの行列の積 g=[[19 24]
[31 38]]
こんなに簡単にベクトルの内積、行列の積が求めれるなんて、素晴らしい。
配列の平均及び標準偏差コード
# 配列の平均及び標準偏差
import numpy as np
# 5から11までのランダムな整数10個の配列
a = np.random.randint(5,12,10)
b = np.mean(a)
c = np.std(a)
print('ランダムな配列a={}'.format(a))
print('平均値b={}'.format(b))
print('標準偏差c={}'.format(c))
input()
(output)
ランダムな配列a=[11 8 8 8 7 9 9 8 7 8]
平均値b=8.3
標準偏差c=1.1
matplotlib
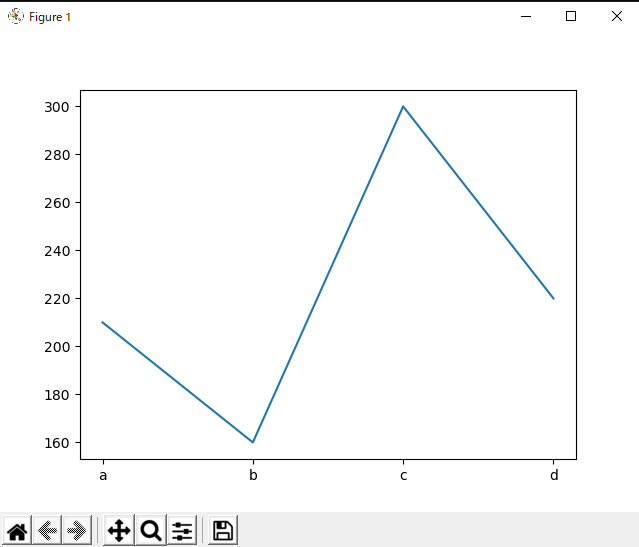
matplotilib基本操作コード
# matplotilib基本操作
import matplotlib.pyplot as plt
x = ['a','b','c','d']
y = [210,160,300,220]
plt.plot(x,y)
plt.show()
input()
sin()関数コード
# sin()関数
import numpy as np
import matplotlib.pyplot as plt
# 0から2πまで
x = np.linspace(0,2*np.pi)
y = np.sin(x)
plt.plot(x,y)
plt.show()
input()
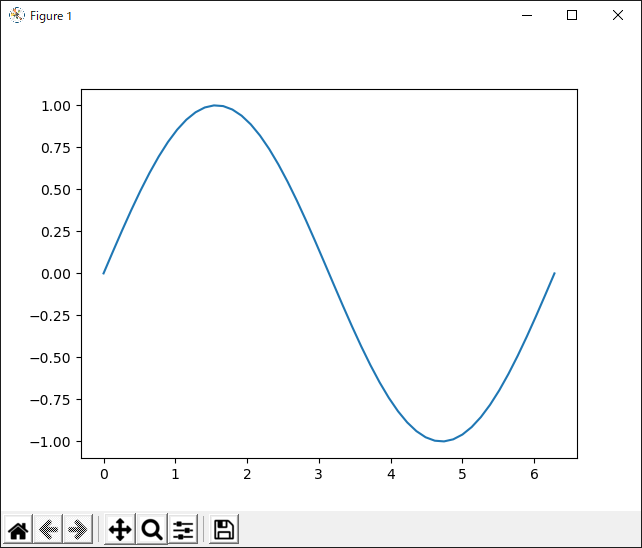
ナイスサインカーブ!
実践
画像認識用のデータ
# 01画像認識用のデータ
from sklearn.datasets import load_digits
digits = load_digits()
a = dir(digits)
b = digits.data.shape
c = digits.target
d = digits.images[0]
e = digits.data[0]
print('digitsデータセットの要素a={}'.format(a))
print('特徴量dataの次元数b{}'.format(b))
print('正解データtargetの値c={}'.format(c))
print('先頭の文字の画像データd={}'.format(d))
print('先頭の文字の特徴量データe={}'.format(e))
(output)
digitsデータセットの要素a=['DESCR', 'data', 'feature_names', 'frame', 'images', 'target', 'target_names']
特徴量dataの次元数b(1797, 64)
正解データtargetの値c=[0 1 2 ... 8 9 8]
先頭の文字の画像データd=[[ 0. 0. 5. 13. 9. 1. 0. 0.]
matplotlibモジュールで表示
# 02matplotlibモジュールで表示
import matplotlib.pyplot as plt
plt.imshow(digits.images[0],cmap=plt.cm.gray_r)
plt.show()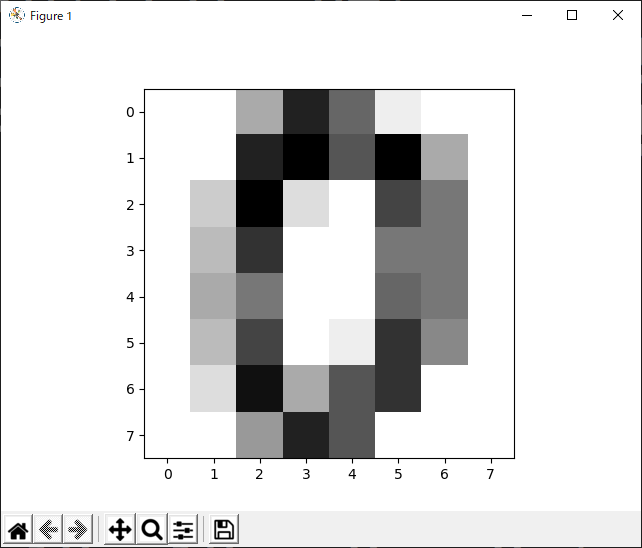
0らしき文字の画像
訓練用データと評価用データの作成
# 03訓練用データと評価用データの作成
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(digits['data'],digits['target'],test_size=0.3,random_state=0)機械学習の実行
# 04機械学習の実行
from sklearn.neural_network import MLPClassifier
# MLPオブジェクトは、多層パーセプトロンと呼ばれる方式により実証されている
mlpc = MLPClassifier(max_iter = 1000)
mlpc.fit(X_train,y_train)機械学習の評価
# 05機械学習の評価
pred = mlpc.predict(X_test)
# 学習モデルが認識した結果がpredに入る
# print(pred)
# 評価用正解データ=y_test
# print(y_test)
print(pred == y_test)
(output)
[ True True True True True True True True True True True True
True True True True True True True True True True True True
True True True True True True True True True True True True
True True True True True True True True True True False True
True True True True True True True True True True True True
True True True True True True True True True True True True
True True True True True True True True True True True True
True True True True True True True True True True True True
True True True True True True True True True True True True
True True True True True True True True True True False True
True True True True False True True True True True True True
True True True True True True True True True True True False
True True True True True True True True True True True True
True True True True True True True True True True True True
True True True True True True True True True True True True
True False True True True True True True True True True True
True True True True True True True True True True True True
True True True True True True True True True True True True
True True True True True True True True True True True True
True True True True True True True True True True True True
True True True True True True True True True True True True
True True True True True True True True True True True True
True True True True True True True True True True True True
True True True True True True True True True True True True
True True True True True True True True True True True True
True True True True True True True True True True True True
True True True True True True True True True True True True
True False True True True True True False True True True True
True True True True True True True True True True True True
True True True True True True True True True True True True
True True True True True True True True True True True True
True True True True True True False True True True True True
True True True True True True True True True True True True
True True False True True True True True True True True True
True True True True True True True True False True True True
True True True True True True True True True True True True
True True True True True True True True True True True True
True True True True True True True True True True True True
True True True True True True True True True True True True
True True True True False True True True True True True True
True True True True True True True True True True True True
True True True True True True True True True True True True
True True True True True True True True True True True True
True True True True True True True True True True True True
True True True True True True True True True True True True]不正解だったらFalseになります。
不正解だった画像を表示
# 06不正解だった画像を表示
import numpy as np
for i, p in enumerate(pred == y_test):
# 比較結果の配列から、インデックスを変数[i]に、要素を変数[p]に入れて繰り返す
if p == False:
plt.title("t:{} p:{}".format(y_test[i],pred[i]))
# tが正解、pが認識結果
img = np.reshape(X_test[i],(8,8))
plt.imshow(img,cmap=plt.cm.gray_r)
plt.show()
# 不正解だった要素のデータを8×8に変換して画像を表示
break
# 不正解を一つ表示したら終了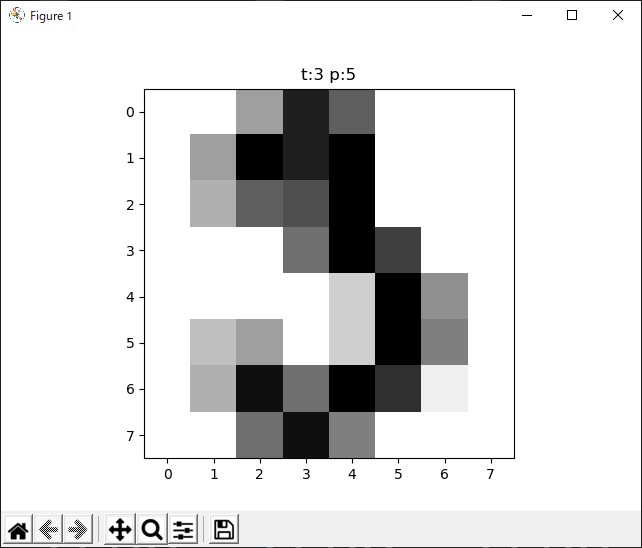
正解tは「3」、認識結果は「5」。
3にも5にも見えますね!
全体の認識精度を評価
# 07全体の認識精度を評価
# np.mean(pred == y_test)
np_mean = np.mean(pred == y_test)
print(np_mean)
from sklearn.metrics import confusion_matrix
c_m = confusion_matrix(y_test,pred,labels=digits['target_names'])
print(c_m)
(output)
0.9796296296296296
[[45 0 0 0 0 0 0 0 0 0] #1の数
[ 0 49 0 0 0 0 1 0 1 1] #2の数 6,8,9で1回ずつ間違えた
[ 0 0 53 0 0 0 0 0 0 0] #3の数
[ 0 0 0 53 0 0 0 0 1 0] #4の数 8で1回間違えた
[ 0 0 0 0 48 0 0 0 0 0] #5の数
[ 0 0 0 0 0 55 1 0 0 1] #6の数 6,9で1回ずつ間違えた
[ 0 1 0 0 0 0 59 0 0 0] #7の数 1で1回間違えた
[ 0 0 0 0 1 0 0 52 0 0] #8の数 4で1回ずつ間違えた
[ 0 2 0 0 0 0 0 0 59 0] #9の数 1で2回間違えた
[ 0 0 0 0 0 0 0 1 0 56]] #10の数 7で1回間違えた正解率は0.979629….
約98%です。
機械学習をやってみた感想
今回は、中島省吾さんが書かれた「知識ゼロでも必ずわかる!ビジネスPython超入門」の本を参考に、
機械学習に挑戦してみました。
ナムペイ、マットプロットリブ等のモジュールの基本的な使い方は理解できましたが、ディープラーニングの詳細はイマイチわかりませんでした。
逆にディープラーニングの詳細を書いていると、初心者は諦めてしまいそうなので、AIに対する好奇心、実際にコードを書いて機械学習をすることができたので、非常に勉強になりました。
次は中級レベルの本を買い、ディープラーニングの詳細を理解したいと思います。
上記本は、機械学習だけではなく、Pythonの基本的な使い方やスプレイピング等、初心者向けの本です。本書の題名通り、知識ゼロでも必ずわかります。
Pythonを始めようと思っている方はぜひ、読んでみてください。
.png)